The Detroit Free Press had a short but interesting story on Friday about the state’s intention to drop Algebra II as a high school graduation requirement. Gov. Jennifer Granholm, a Democrat, has supported such a requirement in the past.
Some state legislators and educators fear it drives up the dropout rate, however, and thus they’d like to see the law amended so that students can opt-out of Algebra II with parental consent. The state senate overwhelmingly approved such a bill on Thursday, and it is now headed to Gov. Granholm’s desk.
The legislator leading the charge was Rep. Joel Sheltrown (D-West Branch), who according to the Free Press article would like to see “an alternative curriculum with such business-oriented math courses as statistics and data analysis.” I wonder, though, just what kind of statistics and data analysis Rep. Sheltrown has in mind — when done well, such courses are by no means easier than Algebra II. In fact, doing statistics and data analysis at a reasonably high level requires a solid grounding in mathematics.
There is definitely an argument to be made for high schools to offer courses in statistics and data analysis, both of which are relevant to our everyday lives and the judgments we make, but their apparent “easiness” is not among them.
Statistics is not for the faint of heart. And yet statistics is hugely important: how else can we decide whether it makes sense to pursue a given course of action? To buy a lottery ticket? (The odds of winning Powerball and MegaMillions are 1 in 195,249,054 and 1 in 175,711,536, respectively.) To believe a research study? To get screened early and often for certain cancers?
Speaking of statistics and cancer, Steven Strogatz recently wrote a blog post in The New York Times called “Chances Are” in which he retold a fascinating story from a book called Calculated Risks by the German cognitive psychologist Gerd Gigerenzer. It turns out most doctors aren’t very good at statistics. Here’s the story, as told by Strogatz:
“In one study, Gigerenzer and his colleagues asked doctors in Germany and the United States to estimate the probability that a woman with a positive mammogram actually has breast cancer, even though she’s in a low-risk group: 40 to 50 years old, with no symptoms or family history of breast cancer. To make the question specific, the doctors were told to assume the following statistics — couched in terms of percentages and probabilities — about the prevalence of breast cancer among women in this cohort, and also about the mammogram’s sensitivity and rate of false positives:
The probability that one of these women has breast cancer is 0.8 percent. If a woman has breast cancer, the probability is 90 percent that she will have a positive mammogram. If a woman does not have breast cancer, the probability is 7 percent that she will still have a positive mammogram. Imagine a woman who has a positive mammogram. What is the probability that she actually has breast cancer?”
Ninety-five out of 100 American doctors “estimated the woman’s probability of having breast cancer to be somewhere around 75 percent,” Strogatz reports.
The correct answer? Nine percent. This, my friends, is the power of statistics. If you’re dying to know why it’s nine rather than 75 percent, read Strogatz’s blog post.
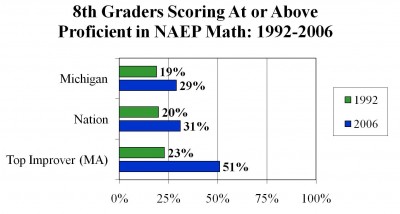Returning to the case of Michigan and Algebra II, it’s worth noting that only 29 percent of the state’s eighth-graders scored at the “proficient” level on the 2006 National Assessment of Educational Progress (NAEP). This is an improvement from the 19 percent of Michigan eighth-graders who scored at the “proficient” level in 1992, but it’s far short of the 51 percent of Massachusetts eighth-graders who were deemed proficient in 2006.
Michigan, like most states, is in desperate need of higher standards — a fact that a school board member quoted in the Free Press article realizes: “[W]e’ve got to have higher standards. We’ve got to have people ready for this type of thinking. The question is, how do we integrate that into the system?” Interestingly, the same school board member offers a very good answer to his own question: “I think the best approach is probably putting in some long-term demands so that we’re integrating this kind of learning right from Day 1, from elementary to middle school to high school.”
Yes, high standards need to be the norm, not the exception, and they need to be in place from the very beginning. There is even some evidence that suggests high standards can actually reduce rather than exacerbate the dropout problem.
